Verify That It Is Orthogonal to Both a and B
We will also work several examples finding the Fourier Series for a function. As part of the GAN series this article looks into ways.

12 4 The Vector A X B Is Orthogonal To Both A And B Youtube
We give some of the basic properties of dot products and define orthogonal vectors and show how to use the dot product.
. Their dot product is 0. These vectors are mutually orthogonal as you may easily verify by checking that v 1 v 2 v 1 v 3 v 2 v 3 0. Orthogonal Diagonalization 425 Theorem 1043 that T is distance preserving if and only if its matrix is orthogonal.
The standard coordinate vectors e 1. This gives you the axis of rotation except if it lies in the plane of the triangle because the translation drops. It works by projecting each vector on the space.
In particular the matrices of rotations and reflections about the origin in R2 and R3 are all orthogonal see Example 821. Pendent vectors and creates a set of n orthogonal vectors. Orthogonal matrices can be easily inverted by just transposing the matrix.
Learn how to verify that a transformation is linear or prove that a transformation is not linear. The dot product veca cdot vecb measures similarity because it. Consider the vectors from R 3.
Standard Empirical Orthogonal Analysis Standard EOF aka eigenvector principal component analysis yields patterns and time series which are both orthogonalThe derived patterns are a function of the domain and the time period being used. Lets verify the first dot. The orthogonal group On is the subgroup of the.
The lack of fit test F Lf of the regression equation is. Prove that eA is an orthogonal matrix ie. Understand the relationship between linear transformations and matrix transformations.
C Complete both of your bases from a to two orthonormal bases A B for R 3 by adding the additional same vector. We now mention some basic and easy-to-verify properties of Gram-Schmidt orthogonalization. The generator produces limited modes and.
I was talking about the cross-product of the changes in the differences between two pairs of vertex positions which would be A-B-A-BtimesB-CtimesB-C. Two vector x and y are orthogonal if they are perpendicular to each other ie. Given a Euclidean vector space E of dimension n the elements of the orthogonal group On are up to a uniform scaling the linear maps from E to E that map orthogonal vectors to orthogonal vectors.
Photo by Andy Beales. In general if B vˆ 1 vˆ 2 vˆ n is an orthonormal basis for a vector space V then the components k i of any vector v relative to B are found from the simple formula Example 14. Taking two vectors we can write every combination of components in a grid.
Representing a function with a series in the form Sum A_n cosn pi x L from n0 to ninfinity Sum B_n sinn pi x L from n1 to ninfinity. Suppose that A is a real n n matrix and that AT A. This completed grid is the outer product which can be separated into the.
In mathematics orthogonality is the generalization of the notion of perpendicularity to the linear algebra of bilinear formsTwo elements u and v of a vector space with bilinear form B are orthogonal when Bu v 0Depending on the bilinear form the vector space may contain nonzero self-orthogonal vectors. The reader can easily verify that 4 and 3 are eigenvalues of A with corresponding eigen-vectors w 1 1 1 and w 2 1. For example matrices consisting of orthogonal column vectors a.
The models do not converge and worse they become unstable. Cross product the interactions between different dimensions xyyz zx etc. Equation and Equation show that the regression equation does not lose fit and the fitting effect is good and has.
A Pore structure viewed along the b axis showing molecular pockets turquoise and the 1D channel yellow. Linear transformations and matrix transformations. First as the name suggests.
Compute the matrix of a linear transformation. C Close-up view of the gourd-shaped aperture connecting the pocket to the channel. 23 F L f S L f f L f S e f e 1897 F 005 92 1938.
Prove that if B eA then BTB I 5. Dot product the interactions between similar dimensions xx yy zz. Is parallel to vec a.
The name of orthogonal group originates from the following characterization of its elements. B Use the Gram-Schmidt process make A and B into orthogonal bases for the plane. A set of orthonormal vectors is an orthonormal set and the basis formed from it is an.
After multiplying by eAteBt on both sides we have eAteBt eABt. Since VU are both integer matrices. In this section we define the Fourier Series ie.
The EOF represntation is optimal in the sense that maximum variance may be accounted for by choosing in order the. The gradient to train the generator vanished. Also it is easier for example to project vectors on subspaces spanned by vectors that are orthogonal to each other.
GAN models can suffer badly in the following areas comparing to other deep networks. 22 F B S B f B S R f R 3514 F 001 5 11 532. In the case of function spaces families of orthogonal.
In linear algebra orthogonal bases have many beautiful properties. It is not enough that the rows of a matrix A are merely orthogonal for A to be an orthogonal. No that would be the cross-product of the changes in two vertex positions.
The regression equation test value F B is. The projection is then the vector that is parallel to vec a starts at the same point both of the original vectors started at and ends where. 3x 4y 3z 0 a Verify that A 4 3 02 3 2 and B 0 3 41 0 1 both.

Answered Verify That It Is Orthogonal To Both A Bartleby
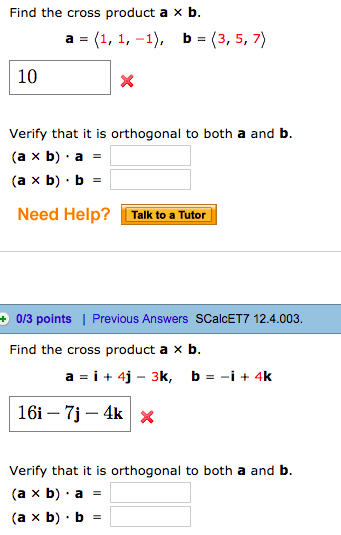
Solved Find The Cross Product A B 10 Verify That It Is Chegg Com

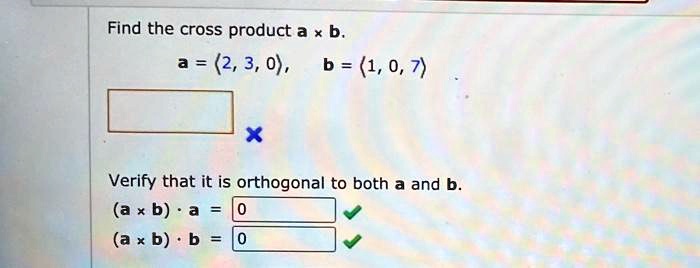
Solved Find The Cross Product A B A 2 3 0 B 1 0 7 Verify That It Is Orthogonal To Both A And B A B A B
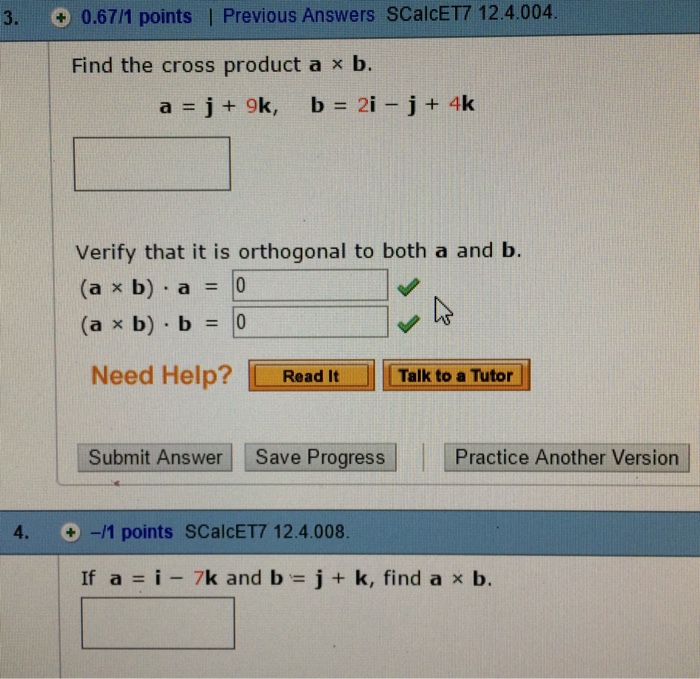
Solved Find The Cross Product A Times B A J 9k B 2i Chegg Com
No comments for "Verify That It Is Orthogonal to Both a and B"
Post a Comment